已知方程(x2-2x+m)(x2-2x+n)=0的4个根组成一个首项为的等差数列，则

问题单项选择题

已知方程(x²-2x+m)(x²-2x+n)=0的4个根组成一个首项为

的等差数列，则|m-n|=( )．

答案

参考答案：C

解析：
因为原方程有4个根，所以方程x²-2x+m=0和x²-2x+n=0各有个两根．又因这两个方程的两根之和都等于2，且这4个根组成等差数列{a_n}，可设这4个根为a₁,a₂，a₃，a₄则有a₁+a₄=a₂+a₃=2．
不妨设上述两方程的根分别为a₁,a₄和a₂，a₃则a₂+a₃=a₁+a₄=2设公差为d，则有2a₁+3d=2．

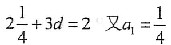
解得

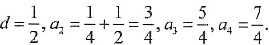
则
故(C)为正确答案．