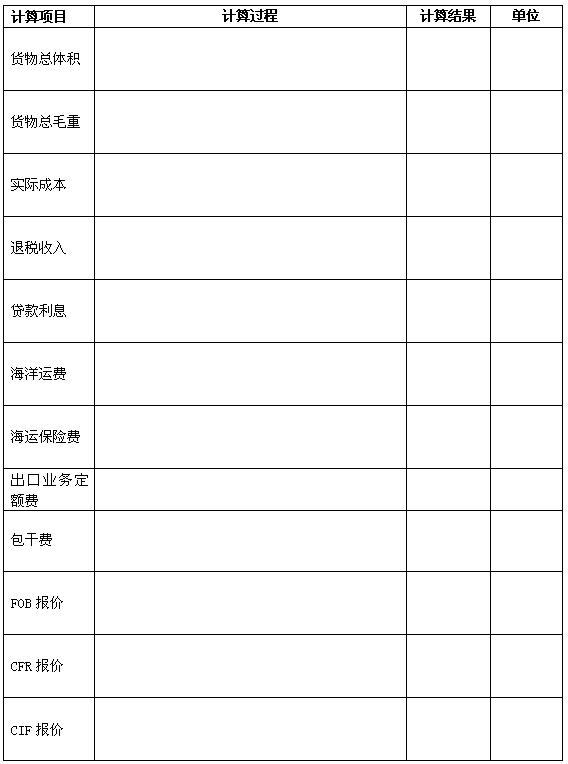
(理)已知函数f(x)=2+
(1)设mn>0,判断函数f(x)在[m,n]上的单调性,并说明理由; (2)设0<m<n且a>0时,f(x)的定义域和值域都是[m,n],求n-m的最大值; (3)若不等式|a2f(x)|≤2x对x≥1恒成立,求a的范围. |
(1)设m≤x1<x2≤n,则f(x1)-f(x2)=-
+1 a2x1
=1 a2x2
,x1-x2 a2x1x2
∵mn>0,m≤x1<x2≤n,∴x1x2>0,x1-x2<0,∴f(x1)-f(x2)<0,
即f(x1)<f(x2),因此函数f(x)在[m,n]上的单调递增.
(2)由(1)及f(x)的定义域和值域都是[m,n]得f(m)=m,f(n)=n,
因此m,n是方程2+
-1 a
=x的两个不相等的正数根,1 a2x
等价于方程a2x2-(2a2+a)x+1=0有两个不等的正数根,
即△=(2a2+a)2-4a2>0且x1+x2=
>0且x1x2=2a2+a a2
>0,1 a2
解得a>
,∴n-m=1 2 1 a
=4a2+4a-3
,-3(
-1 a
)2+2 3 16 3
∵a∈(
,+∞),∴a=1 2
时,n-m最大值为3 2
.4 3 3
(3)a2f(x)=2a2+a-
,则不等式|a2f(x)|≤2x对x≥1恒成立,1 x
即-2x≤2a2+a-
≤2x即不等式对x≥1恒成立,1 x
令h(x)=2x+
,易证h(x)在[1,+∞)递增,同理g(x)=1 x
-2x[1,+∞)递减.1 x
∴h(x)min=h(1)=3,g(x)max=g(1)=-1,
∴
∴-2a2+a≤3 2a2+a≥-1
≤a≤1且a≠03 2