问题
解答题
设锐角三角形ABC的内角A，B，C的对边分别为a，b，c，a=2bsinA，
（Ⅰ）求B的大小；
（Ⅱ）求cosA+sinC的取值范围。
答案
解：（Ⅰ）由a=2bsinA，根据正弦定理得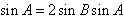
，所以
，
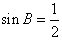由△ABC为锐角三角形得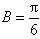
；
（Ⅱ）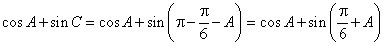
，
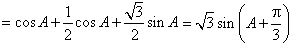由△ABC为锐角三角形知，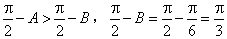
，
，
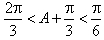所以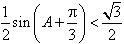
，
由此有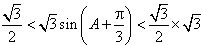
，
所以，cosA+sinC的取值范围为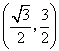
。
搜题请搜索小程序“爱下问搜题”
设锐角三角形ABC的内角A，B，C的对边分别为a，b，c，a=2bsinA，
（Ⅰ）求B的大小；
（Ⅱ）求cosA+sinC的取值范围。
解：（Ⅰ）由a=2bsinA，根据正弦定理得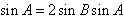，所以，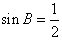
由△ABC为锐角三角形得；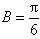
（Ⅱ）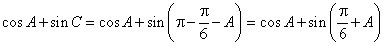
，
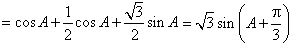由△ABC为锐角三角形知，，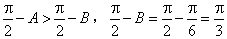
，
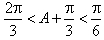所以，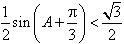
由此有，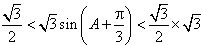
所以，cosA+sinC的取值范围为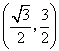。