问题
填空题
菱形ABCD中，AB=4，高DE垂直平分边AB，则BD=______，AC=______．
答案
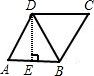
因为DE垂直平分边AB，
所以BD=AD=4
故△ABD和△DBC为等边三角形，
由面积公式得：
AC×BD=AB×DE，1 2
∴AC=2DE=2×4sin60°=4
．BD=4，AC=43
．3
故答案为4，4
．3
搜题请搜索小程序“爱下问搜题”
菱形ABCD中，AB=4，高DE垂直平分边AB，则BD=______，AC=______．
因为DE垂直平分边AB，
所以BD=AD=4
故△ABD和△DBC为等边三角形，
由面积公式得：
AC×BD=AB×DE，1 2
∴AC=2DE=2×4sin60°=4
．BD=4，AC=43
．3
故答案为4，4
．3