问题
解答题
叙述并证明正弦定理．
答案
解：正弦定理：在一个三角形中，各边和它所对角的正弦的比相等． 即
（2R三角形外接圆的直径）
证明：在△ABC中，设BC=a，AC=b，AB=c．
作CH⊥AB垂足为点H CH=a●sinB CH=b●sinA ∴a●sinB=b●sinA
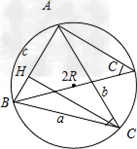
得到
同理，在△ABC中，
，
因为同弧所对的圆周角相等，
所以
，
．
搜题请搜索小程序“爱下问搜题”
叙述并证明正弦定理．
解：正弦定理：在一个三角形中，各边和它所对角的正弦的比相等． 即（2R三角形外接圆的直径）
证明：在△ABC中，设BC=a，AC=b，AB=c．
作CH⊥AB垂足为点H CH=a●sinB CH=b●sinA ∴a●sinB=b●sinA
得到
同理，在△ABC中，，
因为同弧所对的圆周角相等，
所以，．