问题
解答题
在△ABC中，A、B、C所对的三边长分别为a、b、c，若a=2bsinA，求B。
答案
解：∵a=2bsinA，
又由正弦定理得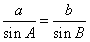
，
∴有sinA=2sinBsinA，
∴2sinB=1，
∴sinB=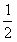
，
∴B=30°或150°。
搜题请搜索小程序“爱下问搜题”
在△ABC中，A、B、C所对的三边长分别为a、b、c，若a=2bsinA，求B。
解：∵a=2bsinA，
又由正弦定理得，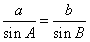
∴有sinA=2sinBsinA，
∴2sinB=1，
∴sinB=，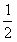
∴B=30°或150°。