问题
选择题
设O为坐标原点，点A（4，3），B是x正半轴上一点，则△OAB中
|
答案
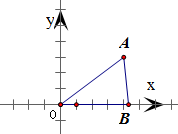
∵A（4，3），
∴根据三角函数的定义，得sin∠AOB=
．3 5
由正弦定理，得
=AB sin∠AOB OB sinA
∴
=OB AB
=sinA sin∠AOB
sinA5 3
由A∈（0，π），得sinA∈（0，1]
∴当A=
时，π 2
=OB AB
sinA的最大值为5 3 5 3
故选：B
搜题请搜索小程序“爱下问搜题”