问题
单项选择题
二维随机变量（X，Y），X～N（0，1），Y～N（0，4），U=X+Y，V=X+2Y，则U、V不相关的充要条件是（）。
A．ρXY=0
B．ρXY=1
C．
D．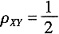
答案
参考答案：C
解析：
考查不相关、协方差的性质。
Cov(U，V)=Cov(X+Y，X+2Y)=Cov(X，X)+Cov(X，2Y)+Cov(Y，X)+Cov(Y，2Y)=D(X)+3Cov(X，Y)+2D(Y)=1+6ρXY+8，上式为0，等价于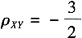
。故正确答案为C。