问题
单项选择题
设y0(x)是微分方程y"+4y'+5y=0满足条件y(0)=-3与y'(0)=2的特解,则
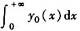
答案
参考答案:A
解析:
[分析]: 二阶常系数线性微分方程y"+4y'+5y=0的特征方程与特征根分别是λ2+4λ+5=0与λ1=-2+i,λ2=-2-i,从而方程y"+4y'+5y=0有两个线性无关的特解y1=e-2xcosx与y2=e-2xsinx,且微分方程的通解为y(x)=C1e-2xcosx+C2e-2xsinx,它的导函数为y'(x)=-(C1+2C2)e-2xsinx+(C2-2C1)e-2xcosx,不难发现无论常数C1与C2取何值都有通解y(x)及其导函数y'(x)满足[*]故
[*]
可见应选(A)。
