问题
单项选择题
设f(x)在[0,2]上连续,并且对任意的x∈[0,1]都有f(1-x)=-f(1+x),则
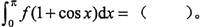
答案
参考答案:B
解析: [*]。因此
[*]
又因为f(1-sin(-t))=f(1+sint)=-f(1-sint),上式最后一步利用了题设条件 f(1-x)=-f(1+x)。所以f(1-sint)是奇函数,奇函数在对称区间上的积分为零,即[*]。
故正确答案为B。
设f(x)在[0,2]上连续,并且对任意的x∈[0,1]都有f(1-x)=-f(1+x),则
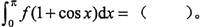
参考答案:B
解析: [*]。因此
[*]
又因为f(1-sin(-t))=f(1+sint)=-f(1-sint),上式最后一步利用了题设条件 f(1-x)=-f(1+x)。所以f(1-sint)是奇函数,奇函数在对称区间上的积分为零,即[*]。
故正确答案为B。