∵AB，BC分别是

3

+

2

，

3

-

2

的等差中项与等比中项，

∴AB=

3

，BC=1，又A=30°，

根据正弦定理

AB

sinC

=

BC

sinA

得：sinC=

3

2

，

∵C为三角形的内角，∴C=60°或120°，

当C=60°时，由A=30°，得到B=90°，即三角形为直角三角形，

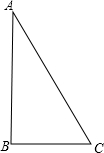
则△ABC的面积为

1

2

×

3

×1=

3

2

；

当C=120°时，由A=30°，得到B=30°，即三角形为等腰三角形，

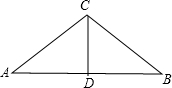
过C作出AB边上的高CD，交AB于点D，

在Rt△ACD中，AC=BC=1，A=30°，∴CD=

1

2

，

则△ABC的面积为

1

2

×

3

×

1

2

=

3

4

，

综上，△ABC的面积为

3

2

或

3

4

．

故选C