参考答案：D

解析：

函数依赖公理：设有关系模式R(U.F)．U为属性全集，F是R的一组函数依赖，X、Y、Z是U的子集。

1)自反律若X包含Y，则有X→Y

2)增广律若X→Y，则有XZ→YZ

3)传递律若X→Y，Y→Z，则有X→Z

推论1 若X→Y，x→z，则有X→YZ

推论2 若X→Y且Z是Y的子集，则有X→Z

推论3 若X→Y，YZ→W，则有XZ→W

若X→Y，Y→Z，由传递律，则X→Z。B项正确。若X→Y，Y→Z，则X→Z，又X→Y，由推论1，则X→YZ。A项正确。若X→Y，Y’是Y的子集，由推论2，则X→Y’。C项正确。若XY→Z，则X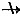z，Y也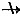Z。所以D项不正确。