解：已知：如图，直线 AB//CD。

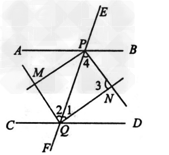
直线EF分别交AB、CD于P、Q。PM平分∠APF。PN平分∠BPF，QM平分∠CQE，QN平分∠DQE。

求证：四边形PMQN为矩形。

证明：∵QM平分∠OQP，

∴∠2=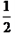∠CQD。

同理可得∠1=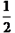∠PQD

∵∠GQP十∠DQP= 180°，

∴ ∠1+∠2=90°，

即∠MQN=90°。

同理可证∠MPN= 90°。

∵AB∥CD。

∴∠BPQ+∠DQP= 180°。   

又PN平分∠BPQ，QN平分∠DQP，    

∴∠1十∠4=  (∠BPQ+∠DQP)=90°。  

∴∠3=90°

∴四边形PMQN为矩形(有三个内角为直角的四边形是矩形)。