解：（1）如正方形、矩形、等腰梯形等，（答案不唯一）；

 （2）结论：等对角线四边形中两条对角线所夹锐角为60^。时，这对60^。角所对的两边之和大于或等于一条对角线的长。

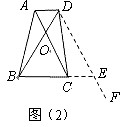
已知：四边形ABCD中，对角线AC，BD交于点O，AC=BD，且∠AOD=60^。

求证：BC+AD≥AC。

证明：过点D作DF∥AC，在DF上截取DE，使DE=AC

连结CE，BE，故∠EDO=60^。，

四边形ACED是平行四边形

所以△BDE是等边三角形，CE=AD

所以DE=BE=AC

①当BC与CE不在同一条直线上时（如图（1）），

在△BCE中，有BC+CE>BE

所以.BC+AD>AC。                 

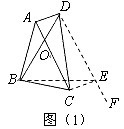
  ②当BC与CE在同一条直线上时（如图（2）），则BC+CE=BE

因此BC+AD=AC

综合①、②，得BC+AD≥AC

即等对角线四边形中两条对角线所夹角为60^。时，这对60^。角所对的两边之和大于或等于其中一条对角线的长。