问题
填空题
点P在圆x2+y2-8x-4y+11=0上，点Q在圆x2+y2+4x+2y-1=0上，则|PQ|的最小值是_ .
答案
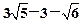
∵已知两圆的圆心坐标分别为
，两圆的半径分别为
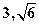，∴|PQ|的最小值＝两圆的圆心距－两圆半径的和＝.
搜题请搜索小程序“爱下问搜题”
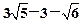点P在圆x2+y2-8x-4y+11=0上，点Q在圆x2+y2+4x+2y-1=0上，则|PQ|的最小值是_ .
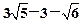
∵已知两圆的圆心坐标分别为，两圆的半径分别为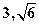，∴|PQ|的最小值＝两圆的圆心距－两圆半径的和＝.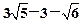