问题
解答题
知圆C1:x2+y2-10x-10y=0和圆C2: x2+y2+6x+2y-40=0相交于A、B两点,求公共弦AB的长.
答案
.
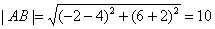由两圆的方程相减,消去二次项得到一个二元一次方程,此方程即为公共弦AB所在的直线方程:4x+3y-10=0.
由
∴A、B的坐标分别是(-2,6)、(4,-2).
故.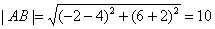
搜题请搜索小程序“爱下问搜题”
知圆C1:x2+y2-10x-10y=0和圆C2: x2+y2+6x+2y-40=0相交于A、B两点,求公共弦AB的长.
.
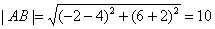由两圆的方程相减,消去二次项得到一个二元一次方程,此方程即为公共弦AB所在的直线方程:4x+3y-10=0.
由
∴A、B的坐标分别是(-2,6)、(4,-2).
故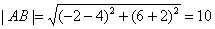.