问题
解答题
已知⊙C：x2+（y-1）2=25，直线l：mx-y+1-4m=0，
（1）求证：对m∈R，直线l与⊙C总有两个不同的交点A，B；
（2）求弦长AB的取值范围；
（3）求弦长为整数的弦共有几条。
答案
解：（1）由mx-y+1-4m=0可得：（x-4）m-y+1=0，
令
，
∴
，
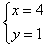∴直线l过定点M（4，1），
又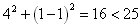
，
∴M（4，1）在⊙C内，
∴直线l与⊙C交于两点；
（2）当直线l过圆心C时，AB取最大值10，此时m=0；
当直线l⊥MC时，AB取最小值，MC=4，
∴
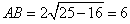，而此时m不存在；
综上有：6＜AB≤10；
（3）由（2）知：6＜AB≤10，
故弦长为整数的值有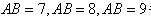
各2有条，
而AB=10时有1条，
故弦长为整数的弦共有7条。