问题
解答题
已知变量y与x成反比例，它的图象过点A（-2，3），
求：（1）反比例函数解析式；
（2）从A（-2，3）向x轴和y轴分别作垂线AB、AC，垂足分别为B、C，则矩形OBAC的面积为_______；
（3）当A点的横坐标为-4时，作AB1、AC1分别垂直于x轴、y轴，B1、C1为垂足，则所得矩形OB1AC1的面积是________；
（4）将A点在图象上任意移动到点A′，作A′B′、A′C′分别垂直于x轴、y轴，B′、C′为垂足，则所得矩形OB′A′C′的面积是_______，
由此，你可以结合上述信息得出结论是：_____________________。
答案
解：（1）∵y与x成反比例，
它的图象过点A（-2，3），代入y=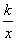
，
∴k=xy=-6，
∴y=
；
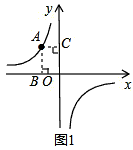
（2）如图1，
∵从A（-2，3）向x轴和y轴分别作垂线AB、AC，
垂足分别为B、C，
∴AC=2，AB=3，
∴矩形OBAC的面积为：2×3=6；
（3）如图2，
∵A点的横坐标为-4，
∴A点的纵坐标为：y=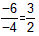
，
∴AB1=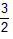
，AC1=4，
∴矩形OB1AC1的面积是：4×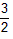
=6；
（4）同理可得出，A点在图象上任意移动到点A′，
作A′B′、A′C′分别垂直于x轴、y轴，B′、C′为垂足，
则所得矩形OB′A′C′的面积是：6；
∴反比例函数图象上的点向坐标轴作垂线与
坐标轴围成的矩形的面积是定值，大小为|k|。