问题
解答题
已知圆的方程为x2+y2=r2,圆内有定点P(a,b),圆周上有两个动点A,B,使PA⊥PB,求矩形APBQ的顶点Q的轨迹方程.
答案
Q的轨迹方程. x2+y2=2r2-(a2+b2),
在矩形APBQ中,连接AB,PQ交于M,
显然OM⊥AB,|AB|=|PQ|,
在Rt△AOM中,若Q(x,y),
则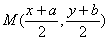 .
.
由|OM|2+|AM|2=|OA|2,
即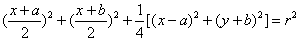 ,
,
也x2+y2=2r2-(a2+b2),这就是Q的轨迹方程.
