已知圆C：x2+y2-2x+4y-4=0，问是否存在斜率为1的直线l，使以l被圆

问题解答题

已知圆C：x²+y²-2x+4y-4=0，问是否存在斜率为1的直线l，使以l被圆C截得的弦AB为直径的圆经过原点，若存在，写出直线l的方程；若不存在，说明理由。

答案

解：假设存在直线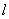，设其方程为y=x+b，

解方程组，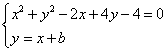

得2x²+(2b+2)x+b²+4b-4=0， ①

设A (x₁，y₁)， B (x₂，y₂)，则x₁+x₂=-b-1，x₁x₂=，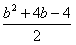

∴y₁y₂=(x₁+b)(x₂+b)=x₁x₂+b(x₁+x₂)+b²=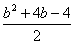+b(-b-1)+b²=，

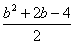又OA⊥OB，

∴x₁x₂+y₁y₂=0，

∴，

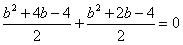解得b=1或b=-4，

把b=1和b=-4分别代入①式，验证判别式均大于0，

故存在b=1或b=-4，

所以存在满足条件的直线方程x-y+1=0 或x-y-4=0。