问题
选择题
已知f(x)=x2+ax-3a-9,对任意x∈R,恒有f(x)≥0,则f(1)的值等于( )
A.3
B.4
C.5
D.6
答案
∵f(x)=x2+ax-3a-9=(x+
)2-a 2
-3a-9,a2 4
因为图象开口向上,
∵f(x)=x2+ax-3a-9,对任意x∈R,恒有f(x)≥0,
∴△≤0,
∴a2-4(-3a-9)≤0,
∴(a+6)2≤0,
∴a=-6,
∴f(1)=12+a-3a-9=-2a-8=-2×(-6)-8=4,
故选B.

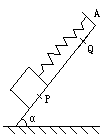
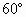 的斜面上,用一根劲度系数k=100N/m的轻弹簧沿平行斜面的方向拉住一个质量为m的物体,如图所示.若发现将物体放在斜面上的PQ之间任何位置都能使之处于静止状态,并测得AP=22cm,AQ=8cm,则物体与斜面间的最大静摩擦力等于多大?
的斜面上,用一根劲度系数k=100N/m的轻弹簧沿平行斜面的方向拉住一个质量为m的物体,如图所示.若发现将物体放在斜面上的PQ之间任何位置都能使之处于静止状态,并测得AP=22cm,AQ=8cm,则物体与斜面间的最大静摩擦力等于多大?