(1)已知函数f(x)=ln(1+x)-
(2)求证:不等式
|
(1)由f(x)=ln(1+x)-a(1-
)知定义域:{x|x>-1}1 x+1
对f(x)求导得:f′(x)=
-1 1+x
=a (x+1)2 x+1-a (x+1)2
①在a≤0时,有x+1-a>0恒成立.故f(x)>0
故此时f(x)在(-1,+∞)上单调递增
②在a>0时,由f'(x)=0知x=a-1
| x | (-1,a-1) | a-1 | (a-1,+∞) |
| f'(x) | - | 0 | + |
| f(x) | ↓ | 极小值 | ↑ |
因此函数在a≤0时,在(-1,+∞)上单调递增;在a>0时,f(x)在(-1,a-1)上为减函数,在[a-1,+∞)上为增函数.…(5分)
(2)要证明:
-1 ln(1+x)
<1 x
在(0,1)上成立.1 2
只需证:
ln(1+x)+ln(1+x)-x>0,在(0,1)上恒成立x 2
设g(x)=
ln(1+x)+ln(1+x)-xx 2
则g′(x)=
(ln(1+x)+x.1 2
)+1 1+x
-1=1 x+1
(ln(1+x)-1 2
)x 1+x
由(1)可知a=1,f(x)在x=0时取到最小值
有ln(1+x)>
,在x>0时恒成立.x 1+x
从而可知g'(x)>0,故g(x)在(0,1)上为增函数∴g(x)>g(0)=0
即:
ln(1+x)+ln(1+x)-x>0恒成立,从而原不等式得证.…(12分)x 2

 、
、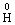 、
、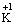 、
、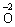 选择适当的元素写出符合下列条件的化学式:①非金属单质 ②氧化物 。
选择适当的元素写出符合下列条件的化学式:①非金属单质 ②氧化物 。