问题
解答题
设直线3x+y+m=0与圆x2+y2+x-2y=0相交于P、Q两点，O为坐标原点，若OP⊥OQ，求m的值。
答案
解：由3x+y+m=0得：y=-3x-m ，
代入圆方程得：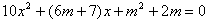
，
设P、Q两点坐标为P（x1，y1）、Q（x2，y2），
则x1+x2=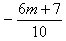
，x1
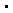x2=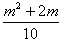
，
∵OP⊥OQ，
∴
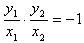，即x1·x2+y1·y2=0，
∴x1·x2+（-3x1-m）（-3x2-m）=0，
整理得：10x1·x2+3m（x1+x2）+m2=0，
∴
，
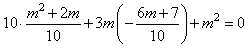解得：m=0或m=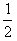
，
又△=（6m+7）2-40（m2+2m）=-4m2+4m+49，
当m=0时，△＞0；
当m=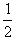
时，△＞0；
∴m=0或m=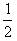
。