问题
解答题
已知曲线C：x2+y2﹣2x﹣4y+m=0．
（1）当m为何值时，曲线C表示圆；
（2）若曲线C与直线x+2y﹣4=0交于M、N两点，且OM⊥ON（O为坐标原点），求m的值．
答案
解：（1）由D2+E2﹣4F=4+16﹣4m=20﹣4m＞0，解得m＜5；
（2）设M（x1，y1），N（x2，y2），
联立直线x+2y﹣4=0与圆的方程x2+y2﹣2x﹣4y+m=0，
消去y，得：5x2﹣8x+4m﹣16=0，
由韦达定理得：
①，
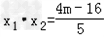②，
又由x+2y﹣4=0得
，
由OM⊥ON得x1x2+y1y2=0，∴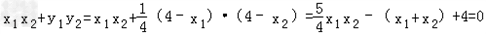
，
将①、②代入上式得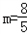 
，检验知满足△＞0，故
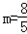为所求．