问题
解答题
考虑坐标平面上以O(0,0),A(3,0),B(0,4)为顶点的三角形,令C1,C2分别为△OAB的外接圆、内切圆.请问下列哪些选项是正确的?
(1)C1的半径为2
(2)C1的圆心在直线y=x上
(3)C1的圆心在直线4x+3y=12上
(4)C2的圆心在直线y=x上
(5)C2的圆心在直线4x+3y=6上.
答案
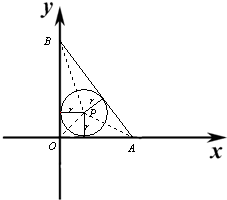
O,A,B三点的位置如右图所示,C1,C2为△OAB的外接圆与内切圆,
∵△OAB为直角三角形,
∴C1为以线段AB为直径的圆,故半径为
|AB|=1 2
,5 2
所以(1)选项错误;
又C1的圆心为线段AB的中点(
,2),此点在直线4x+3y=12上,3 2
所以选项(2)错误,选项(3)正确;
如图,P为△OAB的内切圆C2的圆心,
故P到△OAB的三边距离相等均为圆C2的半径r.
连接PA,PB,PC,可得:S△OAB=S△POA+S△PAB+S△POB
?
×3×4=1 2
×3×r+1 2
×5×r+1 2
×4×r?r=11 2
故P的坐标为(1,1),此点在y=x上.
所以选项(4)正确,选项(5)错误,
综上,正确的选项有(3)、(4).
