问题
解答题
解：已知曲线C：x2+y2﹣4ax+2ay﹣20+20a=0．
（1）证明：不论a取何实数，曲线C必过一定点；
（2）当a≠2时，证明曲线C是一个圆，且圆心在一条直线上；
（3）若曲线C与x轴相切，求a的值
答案
（1）证明：曲线C的方程可变形为（x2+y2﹣20）+（﹣4x+2y+20）a=0．
由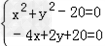
，解得
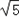
∴点（4，﹣2）满足C的方程，
故曲线C过定点（4，﹣2）．
（2）证明：原方程配方得（x﹣2a）2+（y+a）2=5（a﹣2）2，
∵a≠2，∴5（a﹣2）2＞0
∴C的方程表示圆心是（2a，﹣a），半径是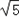|a﹣2|的圆
设圆心坐标为（x，y），
则有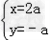
，消去a可得y=﹣
x，
故圆心必在直线y=﹣
x上．
（3）解：由题意得5|a﹣2|=|a|，解得a=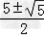
．