问题
解答题
已知圆C:x2+y2+2x﹣4y+3=0.
(1)若圆C的切线在x轴和y轴上的截距相等,求此切线的方程;
(2)从圆C外一点P(x1,y1)向该圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使得|PM|取得最小值的点P的坐标.
答案
解:(1)∵切线在两坐标轴上的截距相等,
∴当截距不为零时,设切线方程为x+y=a,
又∵圆C:(x+1)2+(y﹣2)2=2,
∴圆心C(﹣1,2)到切线的距离等于圆的半径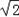 ,即
,即 ,
,
解得:a=﹣1或a=3,
当截距为零时,设y=kx,同理可得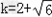 或
或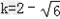 ,
,
则所求切线的方程为x+y+1=0或x+y﹣3=0或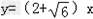 或
或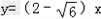 .
.
(2)∵切线PM与半径CM垂直,
∴|PM|2=|PC|2﹣|CM|2.
∴(x1+1)2+(y1﹣2)2﹣2=x12+y12.
∴2x1﹣4y1+3=0.
∴动点P的轨迹是直线2x﹣4y+3=0.
∴|PM|的最小值就是|PO|的最小值.
而|PO|的最小值为原点O到直线2x﹣4y+3=0的距离 ,
,
∴由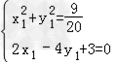 ,
,
可得
P的坐标为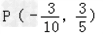 .
.
