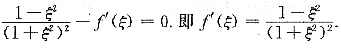问题
问答题
设函数f(x)在区间[0，+∞)上可导，且0≤f(x)≤
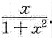
证明：存在ξ＞0，使f’(ξ)=
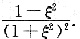
答案
参考答案：
解析： 令
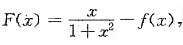由于f(0)=0，所以F(0)=0．
又因为
故由罗尔定理必有ξ∈(0，+∞)，使F’(ξ)=0，即
搜题请搜索小程序“爱下问搜题”
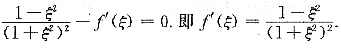
设函数f(x)在区间[0，+∞)上可导，且0≤f(x)≤
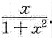
证明：存在ξ＞0，使f’(ξ)=
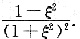
参考答案：
解析： 令
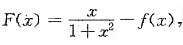由于f(0)=0，所以F(0)=0．
又因为
故由罗尔定理必有ξ∈(0，+∞)，使F’(ξ)=0，即