已知定点A（0，-1），点B在圆F：x2+（y-1）2=16上运动，F为圆心，线

问题解答题

已知定点A（0，-1），点B在圆F：x²+（y-1）²=16上运动，F为圆心，线段AB的垂直平分线交BF于P．

（1）求动点P的轨迹E的方程；

（2）若曲线Q：x²-2ax+y²+a²=1被轨迹E包围着，求实数a的最小值．

答案

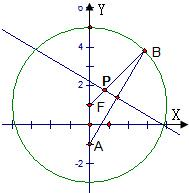
（1）由题意得|PA|=|PB|，

∴|PA|+|PF|=|PB|+|PF|=r=4＞|AF|=2

∴P点轨迹是以A、F为焦点的椭圆．

设椭圆方程为

=1（a＞b＞0），

则2a=4，a=2，a²-b²=c²=1，故b²=3，

∴点p的轨迹方程为

（2）曲线Q：x²-2ax+y²+a²=1化为（x-a）²+y²=1，则曲线Q是圆心在（a，0），半径为1的圆．

而轨迹E：

=1为焦点在y轴上的椭圆，短轴上的顶点(-

，0)，(

，0)

∵曲线Q被轨迹E包围着，则-

+1≤a≤

-1

∴a的最小值为-

+1．