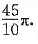问题
问答题
设函数f(x)在[0，1]上连续，在(0，1)内大于0，且满足
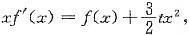又曲线y=f(x)与x=1，y=0所围平面图形σ的面积值等于2，试求y=f(x)，并求常数t为何值时，平面图形σ绕x轴旋转一周所得的旋转体的体积最小．
答案
参考答案：
解析：
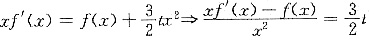
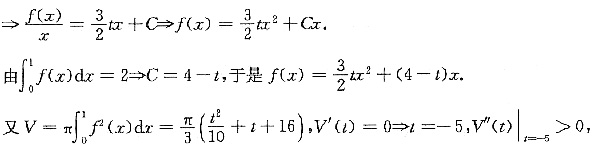
故当t=-5时，所求旋转体体积最小为
搜题请搜索小程序“爱下问搜题”
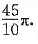
设函数f(x)在[0，1]上连续，在(0，1)内大于0，且满足
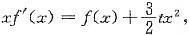又曲线y=f(x)与x=1，y=0所围平面图形σ的面积值等于2，试求y=f(x)，并求常数t为何值时，平面图形σ绕x轴旋转一周所得的旋转体的体积最小．
参考答案：
解析：
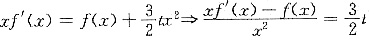
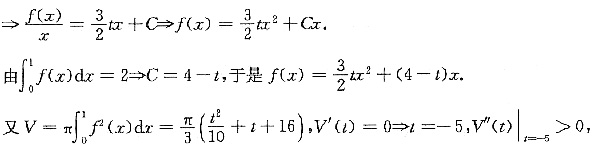
故当t=-5时，所求旋转体体积最小为