问题
填空题
直线x+2y=0被曲线x2+y2-6x-2y-15=0所截得的弦长等于______.
答案
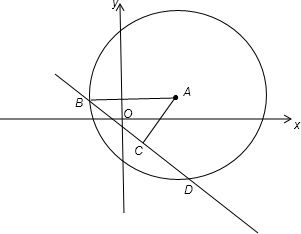
过点A作AC⊥弦BD,垂足为C,连接AB,可得C为BD的中点.
由x2+y2-6x-2y-15=0,得(x-3)2+(y-1)2=25.
知圆心A为(3,1),r=5.
由点A(3,1)到直线x+2y=0的距离AC=
=|3+2| 5
.5
在直角三角形ABC中,AB=5,AC=
,5
根据勾股定理可得BC=
=AB2-AC2
=252-(
)25
,5
则弦长BD=2BC=4
.5
故答案为:45
