问题
填空题
| (坐标系与参数方程选做题) 在极坐标系中,已知点A(1,
|
答案
点A(1,
)的直角坐标为A(0,1),π 2
曲线曲线ρsin2θ=4cosθ的普通方程为y2=4x,是抛物线.
直线ρcosθ+1=0的直角坐标方程为x+1=0,是准线.
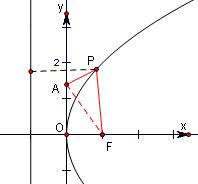
由抛物线定义,点P到抛物线准线的距离等于它到焦点A(0,1)的距离,
所以当A,P,F三点共线时,其和最小,
最小为|AF|=
,2
故答案为:
.2
| (坐标系与参数方程选做题) 在极坐标系中,已知点A(1,
|

点A(1,
)的直角坐标为A(0,1),π 2
曲线曲线ρsin2θ=4cosθ的普通方程为y2=4x,是抛物线.
直线ρcosθ+1=0的直角坐标方程为x+1=0,是准线.
由抛物线定义,点P到抛物线准线的距离等于它到焦点A(0,1)的距离,
所以当A,P,F三点共线时,其和最小,
最小为|AF|=
,2
故答案为:
.2