已知直线l1：（2m+1）x+（m+1）y-7m-5=0（m∈R）和直线l1：x

问题解答题

已知直线l₁：（2m+1）x+（m+1）y-7m-5=0（m∈R）和直线l₁：x+3y-5=0，圆C：x²+y²-2x-4y=0．

（1）当m为何值时，l₁∥l₂？

（2）是否存在点P，使得不论m为何值，直线l₁都经过点P？若存在，求出点P的坐标，若不存在，请说明理由；

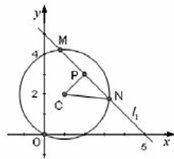
（3）试判断直线l₁与圆C的位置关系．若相交，求截得的弦长最短时m的值以及最短长度；若相切，求切点的坐标；若相离，求圆心到直线l₁的距离的最大值．

答案

（1）∵直线l₁：（2m+1）x+（m+1）y-7m-5=0（m∈R）和直线l₁：x+3y-5=0，l₁∥l₂，

∴3（2m+1）-（m+1）=0

∴m=-

；

（2）直线l₁：（2m+1）x+（m+1）y-7m-5=0（m∈R）可化为（2x+y-7）m+（x+y-5）=0

∴

2x+y-7=0

x+y-5=0

，∴

x=2

y=3

∴存在P（2，3），使得不论m为何值，直线l₁都经过点P；

（3）圆方程化为标准方程为（x-1）²+（y-2）²=5

∴圆心C（1，2），半径为

∴点P到圆心的距离d=

＜

∴P在圆内，∴直线l₁与圆C相交

当直线l₁与直线PC垂直时，截得的弦长最短，最短长度为2

5-|PC|2

此时，

3-2

2-1

•(-

2m+1

m+1

)=-1

∴m=0．