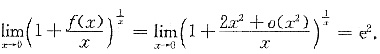问题
问答题
设函数f(x)在点x=0的某邻域内具有二阶导数，
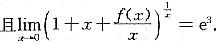求f(0)，f’(0)f’’(0)
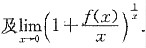
答案
参考答案：
解析： 因为
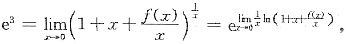
所以
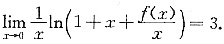
由无穷小比较可知
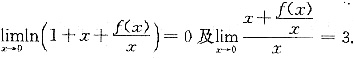
从而
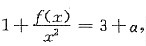其中
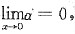即f(x)=2x2+0(x2)，
因此可得f(0)=0，f’(0)=0，f’’(0)=4，并有
搜题请搜索小程序“爱下问搜题”
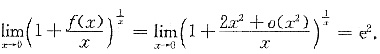
设函数f(x)在点x=0的某邻域内具有二阶导数，
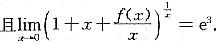求f(0)，f’(0)f’’(0)
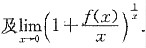
参考答案：
解析： 因为
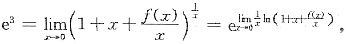
所以
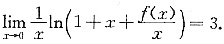
由无穷小比较可知
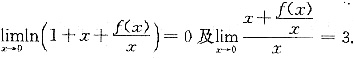
从而
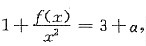其中
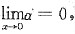即f(x)=2x2+0(x2)，
因此可得f(0)=0，f’(0)=0，f’’(0)=4，并有