问题
解答题
求圆C:(x-1)2+(y+1)2=2上的点与直线x-y+4=0距离的最大值和最小值.
答案
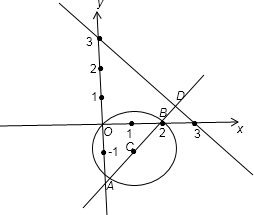
由题意可知当直线AC与直线x-y+4=0垂直时,
垂足为D,且与圆交于A、B两点,此时圆上的点与直线x-y+4=0的最大值为|AD|,
最小值为|DB|,
由圆的方程可得圆心坐标为(1,-1),半径r=|AC|=|BC|=
,2
而圆心C到直线x-y+4=0的距离d=|CD|=
=3|1+1+4| 1+1 2
则圆上的点与直线x-y+4=0距离的最大值|AD|=|AC|+|CD|=
+32
=42
,2
最小值|BD|=|CD|-|CB|=3
-2
=22
.2
