问题
填空题
若圆O1:x2+y2=36与圆O2:(x-m)2+y2=64(m∈R)相交于A、B两点,且两圆在点A处的切线互相垂直,则线段AB的长度是______.
答案
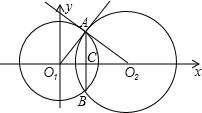
由题意得:圆O1(0,0),r1=6,O2(m,0),r2=8,
∴2<|m|<14,
∵O1A⊥AO2,
∴在Rt△AO1O2中,根据勾股定理得:O1O22=O1A2+O2A2,
即m2=62+82=36+64=100,
∴m=10或m=-10(不合题意,舍去),
则线段AB的长度为2AC=2×
=2×AO1•AO2 O1O2
=6×8 10
.48 5
故答案为:48 5
