问题
解答题
已知圆C:(x-3)2+(y-4)2=4和直线l:x+2y+2=0,直线m,n都经过圆C外定点A(1,0).
(Ⅰ)若直线m与圆C相切,求直线m的方程;
(Ⅱ)若直线n与圆C相交于P,Q两点,与l交于N点,且线段PQ的中点为M,求证:|AM|•|AN|为定值.
答案
(Ⅰ)①若直线m的斜率不存在,即直线是x=1,符合题意.
②若直线m斜率存在,设直线m为y=k(x-1),即kx-y-k=0.
由题意知,圆心(3,4)到已知直线l1的距离等于半径2,
即:
=2,解之得k=|3k-4-k| k2+1
.3 4
所求直线方程是x=1,3x-4y-3=0.
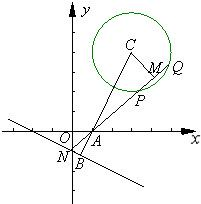
(II)用几何法,如图所示,
△AMC∽△ABN,则
=AM AB
,AC AN
可得|AM|•|AN|=|AC|•|AB|=2
•5
=6,3 5
是定值.
