问题
解答题
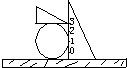
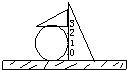
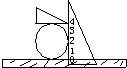
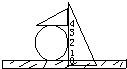
已知与曲线C:x2+y2-2x-2y+1=0相切的直线l与x轴、y轴的正半轴交于两点A、B;O为原点,|OA|=a,|OB|=b(a>2,b>2).
(1)求证:曲线C与直线l相切的条件是(a-2)(b-2)=2;
(2)求△AOB面积的最小值.
答案
(1)证明:直线l的方程为
+x a
=1,即bx+ay-ab=0.y b
曲线C的方程可化为(x-1)2+(y-1)2=1,
所以曲线C为圆.
圆心到直线l的距离d=
,|b+a-ab| a2+b2
当d=1时,直线与圆相切,
即
=1,整理得(a-2)(b-2)=2,|b+a-ab| a2+b2
所以曲线C与直线l相切的条件是:(a-2)(b-2)=2.
(2)由(1)得到(a-2)(b-2)=2且a>2,b>2,
则ab=2(a+b)-2≥4
-2,当且仅当a=b时等号成立,ab
所以当a=b时,ab最小即三角形的面积最小,则三角形AOB为等腰直角三角形
则AB=2(
+1),所以a=b=2
=2 (
+1)2 2
+2,三角形的面积S=2
(1 2
+2)2=3+22 2
所以△AOB的面积的最小值为:3+2
.2