问题
填空题
矩形两条对角线相交的钝角为120°，若对角线长为2，则较短的一边长______．
答案
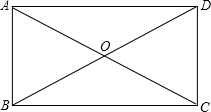
如图，∵矩形的对角线长为2，
∴AO=BO=
×2=1，1 2
∵AC、BD夹角的钝角为120°，
∴∠AOB=60°，
∴△ABO是等边三角形，
∴AB=AO=1，
即较短的一边长1．
故答案为：1．
搜题请搜索小程序“爱下问搜题”
矩形两条对角线相交的钝角为120°，若对角线长为2，则较短的一边长______．
如图，∵矩形的对角线长为2，
∴AO=BO=
×2=1，1 2
∵AC、BD夹角的钝角为120°，
∴∠AOB=60°，
∴△ABO是等边三角形，
∴AB=AO=1，
即较短的一边长1．
故答案为：1．