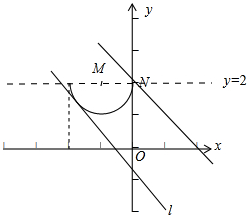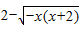解：曲线y=  即，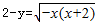

即 （x+1）²+（y-2）²=1，y≤2，表示以M（-1，2）为圆心，半径等于1的半圆（圆位于直线y=2的部分，包括直线y=2上的点），

如图所示：当直线线x+y-m=0过点N（0，2）时，有 0+2-m=0，

解得 m=2．当直线x+y-m=0与半圆相切时，

根据圆心到直线的距离等于半径可得，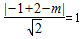

解得 m=1- 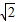，或m=1+  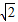（舍去）．

故所求的m的范围为 [1? ，2]，

故选B．