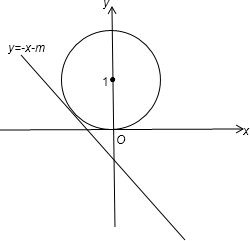
由圆的方程x²+（y-1）²=1得，圆心（0，1），半径r=1

令圆x²+（y-1）²=1与直线x+y+m=0相切，

则圆心到直线的距离d=r，即

|1+m|

1+1

=1，化简得1+m=±

2

，

即m=

2

-1，m=-

2

-1（舍去），

结合图象可知，当m≥

2

-1时，圆上的任一点都能使不等式x+y+m≥0恒成立．

故答案为：[

2

-1，+∞）