问题
选择题
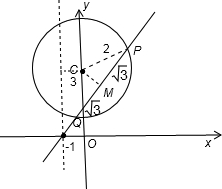
已知定圆C:x2+(y-3)2=4,过点A(-1,0)的一条动直线l与圆C相交于P,Q两点,若|PQ|=2
|
答案
解:由题意画出图形,
如图所示:过圆心C作CM⊥PQ,
则|MP|=|MQ|=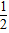 |PQ|=
|PQ|= 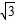 ,由圆C的方程得到圆心C坐标(0,3),半径r=2,
,由圆C的方程得到圆心C坐标(0,3),半径r=2,
在Rt△CPM中,根据勾股定理得:CM=1,即圆心到直线的距离为1,
(i)直线l的斜率不存在时,显然直线x=-1满足题意;
(ii)直线l的斜率存在时,设直线l的斜率为k,
由A(-1,0),得到直线l的方程为y=k(x+1),
即kx-y+k=0,圆心到直线l的距离d=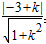 =1,
=1,
解得k=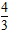 ,所以直线l为4x-3y+4=0,
,所以直线l为4x-3y+4=0,
综上,满足题意的直线l为x=-1或4x-3y+4=0.
故选C