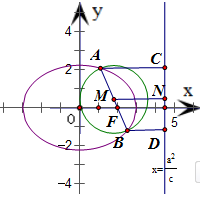
解：设过右焦点F的弦为AB，右准线为l，

A、B在l上的射影分别为C、D 连接AC、BD，

设AB的中点为M，作MN⊥l于N 根据圆锥曲线的统一定义，

可得 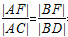 =e，

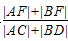可得 =e＜1

∴|AF|+|BF|＜|AC|+|BD|，即|AB|＜|AC|+|BD|，

∵以AB为直径的圆半径为r=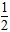 |AB|，|MN|=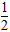（|AC|+|BD|）

∴圆M到l的距离|MN|＞r，可得直线l与以AB为直径的圆相离

故选：C