问题
填空题
在矩形ABCD中,AB=3,BC=4,BE⊥AC于E,则BE=______.
答案
∵四边形ABCD是矩形,
∴∠ABC=90°,
在Rt△ABC中,由勾股定理得:AC=
=5,32+42
则△ABC的面积是S=
×AC×BE=1 2
×AB×BC,1 2
∴
×5×BE=1 2
×3×4,1 2
BE=
,12 5
故答案为:
.12 5
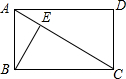
在矩形ABCD中,AB=3,BC=4,BE⊥AC于E,则BE=______.
∵四边形ABCD是矩形,
∴∠ABC=90°,
在Rt△ABC中,由勾股定理得:AC=
=5,32+42
则△ABC的面积是S=
×AC×BE=1 2
×AB×BC,1 2
∴
×5×BE=1 2
×3×4,1 2
BE=
,12 5
故答案为:
.12 5
