问题
解答题
解方程
(1)(x-1)2=4
(2)x2-2x-2=0
(3)x3-2x2-3x=0
(4)x2-4x+1=0(用配方法)
答案
(1)开方得:x-1=±2,
∴x1=3,x2=-1.
(2)这里a=1,b=-2,c=-2,
∵△=4+8=12,
∴x=
=2± 4+8 2
=1±2±2 3 2
,3
∴x1=1+
,x2=1-3
;3
(3)分解因式得:x(x2-2x-3)=0,
即x(x-3)(x+1)=0,
∴x1=0,x2=3,x3=-1;
(4)x2-4x+1=0,
变形得:x2-4x+4-4+1=0,
即(x-2)2=3,
∴x-2=
或x-2=-3
,3
∴x1=2+
,x2=2-3
.3

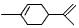 )。下列关于苧烯的说法中,正确的是[ ]
)。下列关于苧烯的说法中,正确的是[ ]