问题
解答题
已知矩形的长大于宽的2倍,周长为12.从它的一个顶点作一条射线,将矩形分成一个三角形和一个梯形,且这条射线与矩形一边所成的角的正切值等于
|
答案
∵矩形ABCD的长大于宽的2倍,矩形的周长为12,
∴AD>4,AB<2,
根据题意,可分为以下两种情况:
第一种情况,如图1,
当tan∠BAE=
时,设CE=x,BE=m,1 2
则AB=DC=2m,AD=m+x,
∵AB+AD=6,
∴2(2m+m+x)=12,
m=
,6-x 3
S梯形AECD=
(AD+EC)•DC,1 2
=
[(m+x)+x]•2m,1 2
=m(m+2x),
=
•6-x 3
,6+5x 3
=-
x2+5 9
x+4,8 3
>0,6-x 3
+x>4,6-x 3
∴x<6,x>3,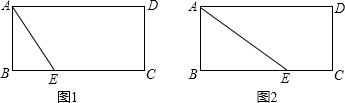
∴x的取值范围是3<x<6;
第二种情况,如图2,
tan∠AEB=
时,1 2
设CE=x,AB=CD=n,
则BE=2n,AD=2n+x,
∵矩形的周长为12,
∴AB+AD=6,
∴2(n+2n+x)=12,n=
,6-x 3
S梯形AECD=
(AD+EC)•DC,1 2
=
[(2n+x)+x]•n,1 2
=n(n+x),
=
•6-x 3
,6+2x 3
=-
x2+2 9
x+4,2 3
∵
>0,2×6-x 3
+x>4,6-x 3
∴x<6,x>0,
∴x的取值范围是0<x<6.
