问题
证明题
求证:顺次连接任意四边形各边中点所得的四边形是平行四边形。(要求画图,写出已知、求证并加以证明)
答案
| 解:已知:在四边形ABCD中,点E,F,G,H分别是边AB,BC,CD,DA的中点。 | |
| 求证: 四边形EFGH是平行四边形。 | |
| 证明:连接AC, | |
| ∵F,G,H分别是边AB,BC,CD,DA的中点。 | |
∴EF∥AC,EF=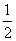 AC HG∥AC,HG= AC HG∥AC,HG= 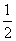 AC AC | |
∴EF∥HG,EF=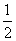 HG HG | |
| ∴四边形EFGH是平行四边形。(一组对边平行且相等的四边形是平行四边形) | 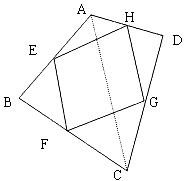 |
