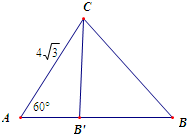
∵△ABC中，A=60°，b=4

3

，

∴作出△ABC的示意图，如图所示

可得点C到直线AB的最短距离为4

3

sin60°=6

以C为圆心，CB长为半径画弧，

则当圆弧与射线AB有且只有一个公共点时，满足条件的△ABC只有一个，

∵当圆弧半径R=6时，圆弧与射线AB相切，有唯一公共点；

当圆弧半径R≥4

3

时，圆弧与直线AB相交有两个交点，但只有一个交点在射线AB上

∴当BC=6或BC≥4

3

时，满足条件的△ABC只有一个，即a≥4

3

或a=6

故选：C