问题
解答题
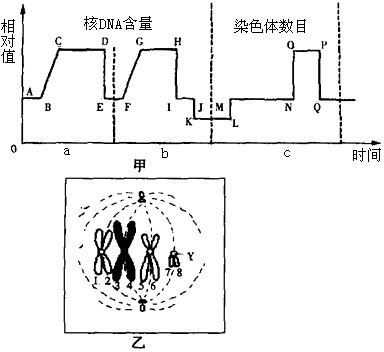
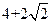△ABC在内角A、B、C的对边分别为a，b，c，已知a=bcosC+csinB．
（1）求B；
（2）若b=2，求△ABC面积的最大值。
答案
（1）
（2）
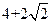
(1)∵a=bcosC+csinB
∴由正弦定理知sinA=sinBcosC+sinCsinB ①
在三角形ABC中，A=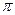
－(B+C)
∴sinA=sin(B+C)=sinBcosC+cosBsinC ②
由①和②得sinBsinC=cosBsinC
而C∈(0，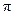
)，∴sinC≠0，∴sinB=cosB
又B(0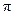，)，∴B=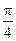
(2)△ABC的面积S=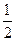
acsinB=
ac
由已知及余弦定理得
4=a2+c2－2accosB ③
而a2+c2≥2ac ④
联立③和④得ac≤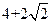，当且仅当a=c时等号成立．
因此△ABC面积的最大值为