问题
解答题
请判断下列命题是否正确?如果正确,请给出证明;如果不正确,请举出反例。
(1)一组对边平行且相等的四边形是平行四边形;
(2)一组对角相等,一条对角线被另一条对角线平分的四边形是平行四边形。
答案
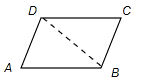
解:(1)已知:如图,在四边形ABCD中,AB∥CD,AB=CD,
求证:四边形ABCD是平行四边形。
证明:连接BD,
∵AB∥CD,
∴∠ABD=∠BDC,
在△ABD和△CDB中,
AB=CD,∠ABD=∠BDC,BD=BD,
∴△ABD≌△CDB(SAS),
∴∠ADB=∠DBC(全等三角形对应角相等),
∴AD∥BC(内错角相等,两直线平行),
∴四边形ABCD是平行四边形;
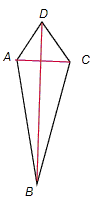
(2)一组对角相等,一条对角线被另一条对角线平分的四边形是平行四边形不正确,
如右图,∠BAD=∠BCD,对角线AC被BD平分,但四边形ABCD不是平行四边形。